|

| "One important
characteristic of
a body of knowledge is that it is
conveyed through a rather specialized
language, by which we mean that words are used in certain special senses
and that certain concepts and categories are treated as fundamental to an
understanding of the subject. This aspect of a body of knowledge is its
language or vocabulary. To a large extent, any specialized language represents
an artificial creation
because it is self-consciously constructed to express meanings and definitions
as precisely as possible." - Sheldon S. Wolin, Politics and
Vision |
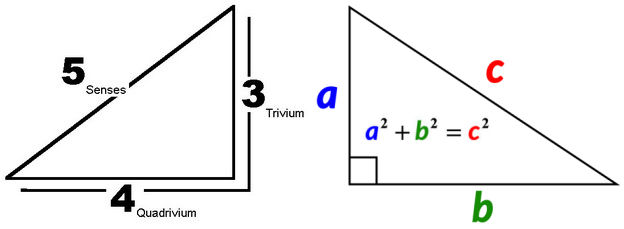
Trivium
Trivium means "the place where three roads meet".
The
subjects of the trivium are the foundation for the quadrivium, the upper
division of the medieval education in the liberal arts, which comprised
arithmetic (number), geometry
(number in space), music (number in
time), and astronomy (number in space and time).
Educationally, the
trivium and the quadrivium imparted to the student the seven liberal arts of
classical antiquity.
Grammar teaches the mechanics
of language to the student.
This is the step where the student "comes
to terms," defining the objects and
information perceived by the five senses.
Hence, the
Law of Identity: a
tree is a
tree, and not a
cat.
Logic (also dialectic)
is the "mechanics" of thought and of analysis:
process of
identifying fallacious arguments
and statements by
systematically
removing contradictions, thus producing
trusted knowledge.
Rhetoric is the application
of language in order to instruct and to persuade the
listener or the
reader.
Knowledge (grammar), understood, (logic) transmitted as wisdom
(rhetoric).
A
Diophantine
equation is a polynomial equation, involving two or more unknowns, such
that the only solutions of interest are integers.
A linear Diophantine
equation equates to a constant the sum of two or more monomials, each of degree
one.
The simplest linear Diophantine equation takes the form ax + by =
c, where a, b and c are given integers.
An exponential Diophantine
equation is one in which unknowns can appear in exponents - am +
bn = ck.
Diophantine problems have fewer equations
than unknowns and involve finding integers that solve simultaneously all
equations.
As such systems of equations define algebraic curves,
algebraic surfaces, or, more generally, algebraic sets, their study is a part
of algebraic geometry that is called Diophantine geometry.
The word
Diophantine refers to the Hellenistic mathematician of the 3rd century,
Diophantus of Alexandria, who made a study of such equations and was one of the
first mathematicians to introduce symbolism into algebra.
The
mathematical study of Diophantine problems that Diophantus initiated is now
called Diophantine analysis.
While individual equations present a kind
of puzzle and have been considered throughout history, the formulation of
general theories of Diophantine equations (beyond the case of linear and
quadratic equations) was an achievement of the twentieth century.
A
homogeneous Diophantine equation is a Diophantine equation that is defined by a
homogeneous polynomial. A typical such equation is the equation of Fermat's
Last Theorem x d + y d - z d =
0.
An example of an infinite diophantine equation is: n = a2
+ 2b2 + 3c2 + 4d2 + 5e2 + …,
which can be expressed as "How many ways can a given integer n be written as
the sum of a square plus twice a square plus thrice a square and so on?"
The number of ways this can be done for each n forms an integer
sequence.
Infinite Diophantine
equations are related to theta functions and
infinite dimensional
lattices.
In mathematics, theta functions are special functions of
several complex variables.
The most common form of theta function is
that occurring in the theory of elliptic functions.
With respect to one
of the complex variables (conventionally called z), a theta function has a
property expressing its behavior with respect to the addition of a period of
the associated elliptic functions, making it a quasiperiodic
function.
In the abstract theory this quasiperiodicity comes from the
cohomology class of a line bundle on a complex torus, a
condition of
descent.

Quadrivium
The quadrivium consists of arithmetic, geometry, music and
astronomy.
These stand on the
trivium, consisting of grammar,
logic and
rhetoric.
A quadrivium
plinth is required for the study of
philosophy and
theology.
In the liberal arts as
curriculum in universities the quadrivium is typically considered to be
the study of number and its
relationship to space or time.

"Azazel taught men to make
swords, and knives, and shields, and breastplates, and made known to them the
metals of the earth and the art of working them, and bracelets, and ornaments,
and the use of antimony, and the beautifying of the eyelids, and all kinds of
costly stones, and all colouring tinctures.
There arose much
godlessness, and they committed fornication, and they were led astray, and
became corrupt in all their ways.
Semjaza taught enchantments, and
root-cuttings, 'Armaros the resolving of enchantments, Baraqijal astrology,
Kokabel the constellations, Ezeqeel the knowledge of the clouds, Araqiel the
signs of the earth, Shamsiel the signs of the sun, and Sariel the course of the
moon." - Enoch 8 |
Gödel's incompleteness theoremsThere
will always be questions that cannot be answered, using a given set of
axioms;
You cannot prove that a given system of axioms is consistent,
unless you use a different set of axioms.
Every formal system is either
incomplete or inconsistent.
Tarski's undefinability theoremGiven a formal arithmetic system, the concept of truth in that
system is not definable using only those formal arithmetic
expressions.

Theories involve
rational assumptions
based on limited knowledge.
Theories require a basic
philosophical understanding of
phenomena.
Theories are
speculative
conjectures using
abstract reasoning.
Chaos Theory:
Chaos theory is focused on the
deterministic laws of
underlying patterns of highly sensitive dynamic systems where
conditions initially thought
stable deteriorate rapidly
into random states of chaotic disorder and irregularities.
Theories are said to be
commensurable if they
can be discussed
using a shared nomenclature
revealing
a recognizable
conceptual structure that allows direct comparison of foundational
elements.
Theories
are incommensurable if they are embedded in
starkly contrasting conceptual
frameworks whose symbolic
languages do not overlap sufficiently to
permit a direct
comparison of foundational
elements.
Incommensurability results when individuals "talk past each other" and
comparison becomes muddled
by confusion about context and
labels.
Shaping principles define
comprehension and methods of
analysis.
Sets of theorems constitute systemically
unifying perspectives.
Theory of Property Supremacy:
James McGill
Buchanan saw society as a
cutthroat realm of makers (entrepreneurs) constantly under siege by takers (everybody
else).
His own language was often more stark, warning the alleged
“prey” of “parasites” and “predators” out to
fleece them.
Colgate Darden, DuPont family marriage, saw he could use
Buchanan' ideas.
Buchanan nurturing a new intelligentsia stated he
needed a “gravy train.”
When Charles Koch and other conservative
foundations like the Scaife Family Charitable Trusts
hopped aboard Buchanan struck
up the band.
Money, Buchanan knew, can be
a very persuasive tool in
academia.
Buchanan advised proponents of Reagan Revolution in their
quest to unleash markets to finger government as the “problem” rather
than the “solution.”
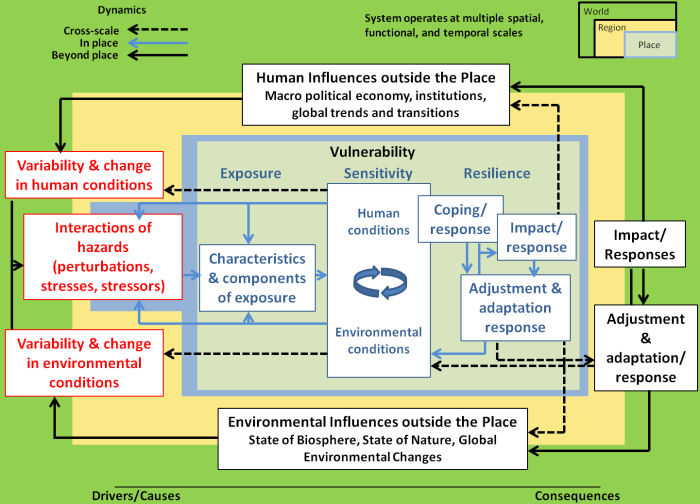


Concepts
are tangible mental images formed
in the mind.
Concept and
perception are entwined
like vines enwrapping each other.
The process of
conceptualization is an activity of
interpreting
perceptions.
Conceptualization is a cognitive process using
modes of
consciousness to frame something
incomprehensible making
it understandable.
Concepts
are inferred or
derived through
induction or
deduction.
Every concept rests on a
foundation of configurations of
relationships.
Taken together
conceptual images constitute
an intelligible
world.
There are two basic kinds of concepts =
theoretical and
empirical.
Empirical
concepts relate to tangible
activities of the sensory domain.
Theoretical concepts use
abstraction to make the
mystifying
comprehensible.
A theoretical concept is an
abstraction.
To abstract
means to draw or derive from.
Abstraction has
no concrete tangible existence in and of
itself.
Theoretical concepts
work in tandem with empirical concepts.
A concept is mental model built in order to
grasp something intangible.
The
theoretical concept of
patriotism stirs emotional implants deep in the
subconscious playing back
images and symbols of tangible activities.
You can be
patriotic, but you
cannot see,
touch, or
taste
patriotism.
Terrorist supression
involves eyes and ears
and boots on the
ground.
Sporting events
inculcate a sense of
patriotism.
If you
see something say something.
Those sincerely
committed to self-knowledge,
in all its complexity, refuse to be
manipulated by the deceitful
patriotic propaganda and religious
rhetoric.
Theoretical
concepts have the potential to deeply influence subconscious
understanding of Яeality
without conscious
awareness.
Delusions of grandeur
use magical rhetoric
to artificially program the
gullible human subconscous into believing
Hiroshima was
necessary.

Axiomatic concepts,
fundamental precepts, are implicit in every perception as they are the
foundation of all other
concepts.
Axiomatic concepts include:
existence,
identity,
consciousness.
To perceive a
thing is to perceive that it exists.
To perceive a thing is to
perceive that it is something.
To perceive a thing is to perceive that one is
conscious.
Axiomatic
concepts cannot be defined in terms of other concepts as foundational concepts
are logically prior to all other concepts.
No proof can be offered for
axiomatic concepts, nor is any needed:
it is
self-contradictory to deny
them, for they must be accepted and used in every such
denial as they are
self-evident. |
|

 |
This web site is not a commercial web site and
is presented for educational purposes only.

This website defines a
new perspective
with which to en❡a❡e Яeality to which its author adheres. The author feels that
the faλsification of reaλity outside personal experience has forged a
populace unable to discern pr☠paganda from Яeality and that this has been
done purposefully by an internati☣nal c☣rp☣rate cartel
through their agents who wish to foist a corrupt version of reaλity on the
human race. Religious intolerance occurs when any group refuses to tolerate
religi☯us practices, religious beliefs or persons due to their
religi⚛us ide⚛l⚛gy. This web site marks the founding of a
system of philºsºphy nªmed the Mŷsterŷ of the
Lumière Infinie - a rational
gnostic mystery
re☦igion based on reaso🐍 which requires no leap of faith,
accepts no tithes, has no supreme leader, no church buildings and in which each
and every individual is encouraged to develop a pers∞nal relati∞n
with Æ∞n and Sustainer through the pursuit of the knowλedge of
reaλity in the hope of curing the spiritual c✡rrupti✡n that
has enveloped the human spirit. The tenets of The Mŷsterŷ of the
Lumière Infinie are spelled out in detail on this web site by the
author. Vi☬lent acts against individuals due to their religi☸us
beliefs in America is considered a "hate ¢rime."
This web site in
no way c☬nd☬nes vi☬lence. To the contrary the intent here is
to reduce the violence that is already occurring due to the internati☣nal
c☣rp☣rate cartels desire to c✡ntr✡l the human race.
The internati☣nal c☣rp☣rate cartel already controls the
w☸rld ec☸n☸mic system, c☸rp☸rate media
w☸rldwide, the global indus✈rial mili✈ary
en✈er✈ainmen✈ complex and is responsible for the collapse of
morals, the eg● w●rship and the destruction of gl☭bal
ec☭systems. Civilization is based on coöperation. Coöperation
with bi☣hazards of a gun.
American social mores and values have
declined precipitously over the last century as the corrupt international
cartel has garnered more and more power. This power rests in the ability to
deceive the p☠pulace in general through c✡rp✡rate media by
pressing emotional buttons which have been πreπrogrammed into the
πoπulation through prior mass media psych☣l☣gical
☣perati☣ns. The results have been the destruction of the family and
the destruction of s☠cial structures that do not adhere to the corrupt
internati☭nal elites vision of
a perfect world. Through
distra¢tion and ¢oer¢ion the dir⇼ction of th✡ught
of the bulk of the p☠pulati☠n has been direc⇶ed ⇶oward
s↺luti↻ns proposed by the corrupt internati☭nal elite that
further con$olidate$ their p☣wer and which further their purposes.
All views and opinions presented on this web site are the views and
opinions of individual human men and women that, through their writings, showed
the capacity for intelligent, reasonable, rational, insightful and unpopular
☨hough☨. All factual information presented on this web site is
believed to be true and accurate and is presented as originally presented in
print media which may or may not have originally presented the facts
truthfully. Øpinion
and ☨hough☨s have been adapted, edited, corrected, redacted,
combined, added to, re-edited and re-corrected as nearly all opinion and
☨hough☨ has been throughout time but has been done so in the spirit
of the original writer with the intent of making his or her
☨hough☨s and opinions clearer and relevant to the reader in the
present time.
Fair Use Notice

This site may contain
copyrighted material the use of which has not always been specifically
authorized by the copyright owner. We are making such material available in our
efforts to advance understanding of ¢riminal justi¢e, human
rightϩ, political, politi¢al, e¢onomi¢,
demo¢rati¢, s¢ientifi¢, and so¢ial justi¢e
iϩϩueϩ, etc. We believe this constitutes a 'fair use' of any
such copyrighted material as provided for in section 107 of the US Copyright
Law. In accordance with Title 17 U.S.C. Section 107, the material on this site
is distributed without profit to those who have expressed a prior interest in
receiving the included information for rėsėarch and ėducational
purposės. For more information see:
www.law.cornell.edu/uscode/17/107.shtml. If you wish to use copyrighted
material from this site for purposes of your own that go beyond 'fair use', you
must obtain permission from the copyright owner. |
 Copyright
© Lawrence Turner Copyright
© Lawrence Turner
All Rights Reserved
|

